Materi dalam pelajaran matematika sering dijumpai dalam kehidupan sehari-hari, seperti bilangan berpangkat misalnya. Pengertian bilangan berpangkat adalah jenis bilangan yang dikalikan dengan angka itu sendiri berkali-kali.

Misalnya, dua pangkat empat, maka angka dua akan dikalikan dengan dua sebanyak empat kali. Hasil perhitungan angka berpangkat tersebut biasanya dipergunakan dalam berbagai perhitungan ilmu fisika, contohnya kecepatan cahaya, massa elektron, jarak bumi dan matahari dan lainnya.

Bilangan yang dipangkatkan terdiri dari beberapa jenis dan sifat, yang akan menentukan hasil akhir dari perhitungannya. Karena fungsinya tidak hanya sebatas sebagai teori dalam matematika saja, maka pengertian angka yang dipangkatkan sebaiknya dipahami dengan benar.

Apakah Bilangan Berpangkat Itu?

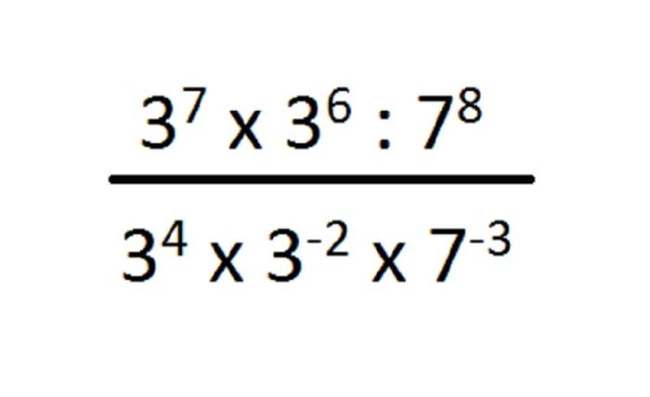
Dalam buku kelas IX SMP/ MTS berjudul Explore Matematika III, oleh Agus Supriyanto dan Miftahudin, yang disebut sebagai bilangan berpangkat adalah hasil perkalian sebuah angka atau bilangan dengan dirinya sendiri, atau dengan angka yang sama, berkali-kali.

Pangkat terkecil yaitu pangkat dua hingga tidak terkira dan harus berupa bilangan bulat. Jadi, tidak bisa angka pecahan dipangkatkan ataupun angka bulan dipangkatkan dengan angka pecahan. Jika bilangannya berupa angka pecahan, maka namanya angka berpangkat pecahan.

Karena dikalikan dengan dirinya sendiri, maka dapat disebut juga sebagai perkalian berulang. Misalnya 2 pangkat 4 maka bentuknya akan menjadi 2x2x2x2, begitu juga dengan angka-angka yang lainnya.

Bilangan yang dipangkatkan bisa berupa angka positif maupun negatif. Pada pelajaran matematika untuk siswa SMA, bilangan yang dipangkatkan juga disebut sebagai eksponen. Fungsi eksponen adalah untuk memudahkan penulisan bilangan yang melibatkan banyak angka.

Sifat Bilangan Berpangkat

Bilangan dengan pangkat atau eksponen memiliki beberapa sifat, yang dapat dilihat dalam penjelasan berikut ini.

1. Penjumlahan Pangkat

Penjumlahan pangkat adalah dua atau lebih bilangan yang dipangkatkan menggunakan basis yang sama. Jika menjumpai bilangan seperti ini, maka tinggal dijumlahkan saja pangkat pada bilangan tersebut.

Namun, penjumlahan seperti ini hanya dapat dipakai jika angka yang dipangkatkan memiliki basis yang sama, misalnya 4. Tapi jika basisnya berbeda, sifat penjumlahan pangkat tidak dapat dilakukan, harus menggunakan rumus lainnya yang sesuai.

Contoh eksponen dengan basis angka yang sama, yaitu :

4⁴+ 4⁶= 4⁴⁺⁶ = 4¹⁰
5²+ 5³ = 5²⁺³= 5⁵

Dalam kedua contoh diatas, basis angkanya sama, yaitu 4 dan 5.

2. Pengurangan Pangkat

Hampir sama dengan penjumlahan pangkat, hanya saja pada sifat ini, angka pangkat dikurangkan. Syaratnya tidak berbeda dengan sifat penjumlahan pangkat, basis angkanya harus sama. Contohnya seperti berikut :

Rumus : a^b/ a^c = a^b-c, dimana b>c,
Perhitungannya : 4³/ 4²= 4^3-2

Rumus ini berlaku untuk semua bilangan berpangkat dengan sifat pengurangan dima basis angkanya sama.

3. Perkalian Pangkat

Sifat eksponen yang selanjutnya adalah perkalian pangkat. Apa maksudnya? Sifat perkalian pangkat ini berlaku pada eksponen yang dipangkatkan lagi. Atau diterapkan pada perkalian antar bilangan yang mempunyai pangkat sama. Lebih jelasnya lihat berikut ini.

Rumus : (a^b)^c= a^bxc
Contoh : (3²)² = 3^2×2= 3⁴

Jika diperhatikan, maka pada rumus sifat perkalian pangkat tersebut juga berlaku jika basis angkanya sama.

4. Pangkat Satu

Jika suatu eksponen dipangkatkan satu (x¹), maka hasil perhitungannya akan sama dengan bilangan basisnya itu sendiri. Angka berapa saja yang menjadi basisnya, jika dipangkatkan dengan angka 1, maka hasilnya bilangan itu sendiri.

Contohnya : 5¹ maka artinya 5×1 = 5, begitu juga dengan bilangan-bilangan yang lainnya. Selama dipangkatkan dengan notasi 1, maka hasilnya akan sama dengan bilangan basisnya.

5. Pangkat Nol

Berapakah hasil perkalian dengan nol? Berapapun bilangan yang dikalikan nol maka hasilnya sama dengan nol (0). Namun, untuk sifat eksponen sifatnya agak berbeda, yaitu berapapun bilangan basis yang dipangkatkan nol maka hasilnya adalah 1.

Kenapa hasil akhir pangkat nol selalu satu? Alasannya adalah berapapun angka yang dipangkatkan dengan angka no (x⁰), maka hasilnya menjadi tidak terdefinisi, maka ditulis dengan angka 1. Contoh : 6⁰ = 1, 8⁰ =1 dan seterusnya.

6. Pangkat Negatif

Bilangan berpangkat negatif nilainya akan sama dengan 1 pada setiap eksponen yang berubah menjadi pangkat positif. Lebih jelasnya dapat dilihat pada rumus dan contohnya berikut ini.

7. Pembagian Pangkat atau Pangkat Pecahan

Pada sifat ini, maka artinya sama dengan eksponen yang diakarkan. Saat menjumpain bilangan seperti ini, maka yang dibagi hanya pangkatnya saja, tidak perlu dengan bilangan basisnya. Rumus dan contohnya yaitu :

Jenis- Jenis Bilangan Berpangkat

Secara umum, bilangan yang dipangkatkan atau eksponen terdiri dari dua jenis, yaitu positif dan negatif. Bagaimanakah maksudnya? Positif dan negatif dapat dilihat pada tanda yang terdapat pada angka pangkatnya (x³_,x^-3). Penjelasannya adalah sebagai berikut :

1. Bilangan dengan Pangkat Positif

Bilangan dengan pangkat positif adalah eksponen yang mempunyai pangkat merupakan bilangan positif. Misalnya, 3², 4²_,5⁵dan seterusnya, dimana jika angka pangkatnya makin besar maka makin besar juga nilai pada bilangan tersebut.

2. Bilangan dengan Pangkat Negatif

Jika suatu bilangan eksponen memiliki pangkat dengan tanda negatif pada pangkatnya (x^-a), maka disebut sebagai pangkat negatif. Contohnya, 2^-3, 4^-4, 5^-2 dan seterusnya, dimana kalau angka di belakang tanda negatif (-) makin besar, maka nilai bilangannya akan semakin kecil.

Rumus Umum Bilangan Berpangkat

Dalam materi pelajaran matematika akan diajarkan bagaimana rumus pada bilangan berpangkat atau eksponen. Adapun bentuk umum rumus bilangan eksponen yaitu :

Rumus : x^a dengan x tidak sama dengan 1 dan a R

Maka dari rumus yang dituliskan di atas, maka x merupakan bilangan basis, dan a adalah pangkatnya atau eksponen.

Syarat yang berlaku pada rumus bilangan eksponen ini yaitu, bilangan basis tidak boleh sama dengan 1 (satu), karena angka 1 dipangkatkan atau dengan bilangan apapun hasilnya sama, yaitu satu (1).

Sedangkan syarat yang kedua yaitu angka pada pangkatnya berupa bilangan real, baik positif maupun negatif. Contoh bilangan real misalnya 2,3,4,5 ataupun -2,-3,-4,-5 dan seterusnya.

Contoh Soal Bilangan Berpangkat

Supaya pemahaman tentang bilangan eksponen makin jelas, silahkan lihat beberapa contoh di bawah ini.

1. Contoh 1

Adi membeli tali untuk lomba tarik tambang di kampungnya. Tali yang dibelinya tersebut memiliki ukuran panjang x⁴meter dan lebarnya x² meter. Hitung berapakah selisih ukuran panjang dan lebarnya, jika luas tali tambang yang dibeli Adi yaitu 4m².

Untuk menjawab persoalan tersebut, maka harus dilakukan perhitungan sebagai berikut :

p = x⁴ dan l = x²
L = 4m²
Berapa selisih panjang dan lebarnya?

Perhitungannya yaitu :

L = pxl
4 = x^4-2
Maka x = 2

Setelah itu, masukkan hasil x = 2 pada rumus persamaan panjang dan lebar.

p = x⁴ = 2³ = 8
l = x^-2 = 0,25 meter

Jadi, dari hasil perhitungan diketahui bahwa panjang tambang adalah 8 meter dan lebarnya 0,25 meter. Jika dihitung selisihnya, maka 8-0,25 didapatkan hasil 7,75.

2. Contoh Soal 2

Hitunglah berapa nilai yang dapat memenuhi persamaan di bawah ini :

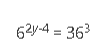
Maka cara menghitungnya adalah samakan dulu bilangan basisnya yang ada di sebelah kiri dan sebelah kanan. Basis yang tepat dan digunakan adalah angka 6, sehingga perhitungannya sebagai berikut :

6^2y-4 = 36³
6^2y-4= (6²)³= 6⁶
2y-4 = 6
2y = 6+4 =10
y = 5

Jadi, nilai yang dicari dari persamaan di atas yaitu 5.

Penerapan Bilangan Berpangkat dalam Kehidupan Sehari-Hari

Bilangan eksponen atau berpangkat bukan sekedar materi dalam matematika saja, tetapi banyak ditrerapkan dalam kehidupan sehari-hari. berikut ini adalah contoh penggunaan bilangan berpangkat dalam kehidupan sehari-hari.

1. Penerapan dalam Bidang Militer

Bilangan eksponen digunakan dalam bidang militer dengan fungsi yang cukup penting, yaitu untuk memperhitungkan jarak akurasi tembakan meriam, yang lintasan tembakannya serupa dengan bentuk parabola.

Sementara itu, pada persamaan fungsi parabola, rumus yang digunakan mengandung eksponen didalamnya.

2. Penerapan dalam Bidang Arsitektur

Ilmu arsitektur yang merupakan bagian dari teknik juga menggunakan bilangan berpangkat dalam perhitungan luas bidang datar, lingkaran dan juga bujur sangkar. Bilangan eksponen juga diperlukan ketika menghitung volume tabung, kubus, bola dan kerucut.

3. Penerapan dalam Bidang Ekonomi

Contoh penerapan bilangan pangkat di bidang ekonomi yaitu untuk memperkirakan nilai uang pada masa yang akan datang. Dengan mengetahui berapa nilai mata uang masa depan, maka dapat membuat prediksi tentang inflasi dan bagaimana antisipasi untuk menghadapinya.

Sedangkan manfaat pada ekonomi mikro yaitu untuk mengetahui berapa nilai tukar suatu mata uang terhadap barang. Keuntungannya yaitu dapat digunakan untuk mengetahui apakah nilai investasi di masa depan dapat memberikan prospek yang baik atau justru sebaliknya.

4. Penerapan dalam Bidang Statistik

Bilangan eksponen atau berpangkat juga diterapkan dalam bidang statistik. Kegunaan bilangan tersebut pada bidang statistik yaitu untuk melakukan uji t ataupun z, pada data sebaran dengan distribusi normal pada ilmu statistik.

5. Penerapan dalam Bidang Lainnya

Selain dalam berbagai bidang yang telah disebutkan di atas, fungsi bilangan berpangkat juga sangat dibutuhkan pada bidang lainnya. Diantaranya yaitu :

Peternakan : Untuk melakukan perkiraan atau prediksi pada hasil ternak dengan memakai konsep geometri atau rasio.
Perdagangan : Untuk memperhitungkan nilai keuntungan dan kerugian dengan menggunakan kuantitas serta harga barang sebagai acuannya.
Kimia : Untuk mencari berapa pH atau tingkat keasaman dari suatu larutan.
Fisika : Untuk mencari berapa nilai induksi magnetik yang terjadi pada suatu kumparan magnet.

Masih banyak lagi bidang-bidang lainnya yang menggunakan konsep dasar bilangan eksponen dalam perhitungannya, misalnya luas tanah dan sebagainya.

Bilangan berpangkat yang disebut juga bilangan eksponen merupakan bilangan yang dikalikan secara berulang-ulang. Oleh sebab itu, bilangan eksponen disebut juga sebagai perkalian berulang, dimana bilangannya harus real dan angka basisnya lebih dari satu (1).

Bilangan berpangkat terdiri dua jenis dan memiliki sifat-sifat yang berbeda. Setiap sifat eksponen mempunyai rumus dan cara perhitungan masing-masing. Bukan sekedar menjadi materi dalam matematika saja, bilangan eksponen juga sangat banyak fungsinya dalam kehidupan sehari-hari.

Baca Juga: