Dalam ilmu matematika ada banyak jenis operasi hitung, salah satunya adalah penjumlahan. Tentu sangat mudah jika hanya menghitung 1+2+3+4+5+6, dengan cara manual pun bisa dilakukan. Tapi bagaimana kalau deret angkanya sampai ratusan atau ribuan? Dalam hal ini diperlukan notasi sigma.
Bisa dibayangkan jika harus menulis penjumlahan dengan deret angka sampai ratusan atau ribuan secara manual, pasti akan sangat panjang dan membingungkan. Untuk memahami lebih jauh tentang materi tersebut, silakan simak pembahasan berikut.
Pengertian Notasi Sigma

Sebelum membahas lebih jauh tentang materi tersebut, harus diketahui bahwa sigma sendiri dilambangkan dengan simbol ∑. Simbol tersebut mungkin masih belum begitu familiar bagi banyak orang, dan mungkin tidak sedikit yang membacanya dengan huruf E, padahal itu adalah sigma.
Asal mula simbol ∑
Simbol sigma diketahui berasal dari susunan huruf alfabet Yunani yang ke-18 dan dibaca sebagai huruf S dalam Bahasa Latin. Sementara Bangsa Yunani menggunakannya sebagai simbol SUM atau penjumlahan deret angka.
Dalam ilmu matematika maupun ilmu pengetahuan alam, simbol ∑ atau sigma digunakan untuk menunjukkan penjumlahan. Sebagai informasi, simbol ∑ pertama kali digunakan oleh seorang ahli matematika asal Swiss yang bernama Leonhard Euler pada tahun 1755.
Definisi ∑
Simbol tersebut dipilih karena menunjukkan istilah SUM yang diawali dari huruf S dan memiliki simbol ∑ atau sigma dalam Bahasa Yunani. Jika merujuk pada fungsi dari simbol tersebut, maka dapat disimpulkan bahwa yang dimaksud notasi sigma adalah:
Suatu bentuk penulisan yang bertujuan untuk meringkas penjumlahan suku-suku yang ada dalam suatu deret angka. Suku-suku dalam penjumlahan tersebut mengikuti pola tertentu sehingga tidak bisa dengan pola acak.
Materi ini juga berkaitan erat dengan materi deret dan barisan di geometri dan aritmatika. Oleh karena itu, agar lebih mudah dalam memahami, sebaiknya Anda sudah menguasai materi tentang baris dan deret yang ada di geometri maupun aritmatika.
Rumus Notasi Sigma
Untuk melakukan penjumlahan dengan menggunakan sigma, maka diperlukan rumus dasar yang berguna untuk perhitungan tersebut. Sebenarnya rumus dasar untuk penjumlahan ini cukup sederhana, namun sayangnya banyak yang kurang memahami sehingga terkecoh dan salah dalam menjawab.
Secara umum rumus yang digunakan pada perhitungan ini adalah:

Keterangan:
∑ adalah Notasi Sigma
Ui adalah formula atau suku ke-i
i adalah indeks penjumlahan
p adalah batas bawah dari indeks penjumlahan
n adalah batas atas dari indeks penjumlahan
Untuk keterangan lebih lengkapnya adalah seperti berikut:
- Batas atas merupakan angka terakhir dalam penjumlahan yang harus dicapai sedangkan batas bawah merupakan angka pertama dalam penjumlahan yang digunakan untuk memulai perhitungan.
- Formula atau suku ke-i merupakan persamaan yang akan digunakan dalam setiap indeks, baik pada indeks batas bawah maupun indeks batas atas. Sementara indeks penjumlahan merupakan indeks yang nantinya akan dimasukkan dalam formula sebagai variabel.
Untuk memudahkan dalam menghitung sigma, Anda juga perlu memahami kembali materi tentang FPB dan KPK yang dipelajari dalam matematika dasar.
Dalam hal ini, notasi sigma juga harus mengacu pada rumus umum yang sudah ada, seperti pada penjelasan berikut:

Berdasarkan bentuk umum diatas, maka diketahui bahwa:
Ui = 2i + 5
Itu artinya Anda perlu menjumlahkan semua suku yaitu (2i + 5)untuk i = 1 sampai i =5. Dengan demikian maka perhitungannya adalah:
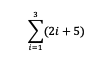
= (2(1) + 5) + (2(2) + 5) + (2(3) + 5) + (2(4) + 5) + (2(5) + 5)
= 7 + 9 + 11 +13 + 15
= 55
Sifat-Sifat Notasi Sigma

Untuk lebih memahami tentang materi pelajaran matematika ini maka Anda bukan hanya menghafalkan rumus dasarnya saja tetapi juga perlu memahami apa saja sifat-sifat dari rumus tersebut. Sehingga nantinya bisa menerapkan rumus yang paling tepat dalam perhitungannya.
Untuk lebih jelasnya, berikut ini akan dijelaskan secara detail bagaimana sifat-sifat yang ada pada perhitungan notasi sigma:
- Sifat pertama ditunjukkan dengan rumus berikut:
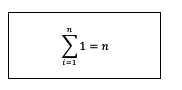
Sifat diatas menunjukkan bahwa dalam penjumlahan tersebut suku yang nilainya 1 pada indeks i = 1 sampai n maka akan menghasilkan angka n itu sendiri. Adapun contohnya adalah seperti berikut:
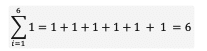
- Sifat yang kedua yaitu:
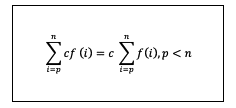
Dalam rumus tersebut dapat diketahui bahwa sifat dari notasi sigma ini menunjukkan adanya konstanta sehingga tidak perlu dimasukkan dalam operasi penjumlahan secara langsung.
Nantinya konstanta yang ada di depan suku bisa dikalikan setelah hasil akhir penjumlahan ditemukan. Berikut ini contohnya:
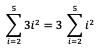
= 3 (22 + 32 + 42 + 52)
= 3 (4 + 9 + 16 + 25)
= 3 (54)
= 162
- Sifat yang ketiga adalah seperti berikut:
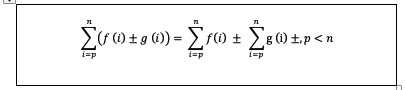
Sifat notasi sigma diatas berlaku untuk jenis penjumlahan dua suku yang berlainan. Jika menjumpai soal seperti diatas, maka Anda perlu mencari hasil penjumlahan dari masing-masing suku yang ada.
- Sifat yang keempat adalah:
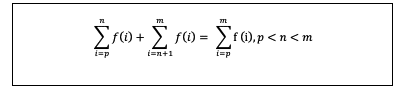
Sifat tersebut menunjukkan bahwa dua sigma diatas memiliki rumus dengan suku yang sama namun batas yang berbeda. Adapun ketentuannya adalah batas bawah dari sigma yang kedua merupakan n+1 atau merupakan lanjutan dari batas atas sigma pertama.
Dengan demikian maka pada sigma yang baru akan didapatkan batas bawah sama seperti sigma yang pertama sedangkan batas atasinya sama seperti sigma yang kedua. Berikut ini contohnya:
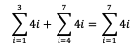
dan lainnya.
Penjelasan Lain Mengenai Sifat Notasi Sigma
Perlu diketahui bahwa dalam mempelajari materi tentang sigma ini Anda perlu mengetahui apa saja sifat-sifat yang ada di dalamnya. Seperti bisa diubah indeksnya maupun diubah dalam penulisan notasinya. Agar tidak bingung, berikut ini pembahasannya:
1. Penulisan Indeks Bisa Diubah
Pada dasarnya penulisan indeks pada sigma ini tidak harus menggunakan huruf i, Anda bisa saja mengubahnya menjadi huruf a, k atau l. Namun harus dipastikan jika huruf indeksnya sudah diubah, maka pada kalimat matematikanya penulisan huruf indeks juga harus sama.
Selain itu, huruf yang telah digunakan untuk mengubah indeks tidak boleh sama dengan huruf yang akan digunakan untuk menunjukkan batas atas dari sigma tersebut. Berikut ini contohnya:
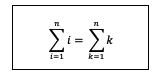
2. Bentuk Notasi Sigma Bisa Diubah
Bukan hanya indeksnya saja yang bisa diubah, dalam notasi sigma ini Anda juga bisa mengubah bentuknya dengan cara dipisahkan menjadi dua penjumlahan atau lebih. Berikut ini beberapa contohnya:
- Dipisahkan menjadi dua penjumlahan atau lebih

Dari contoh diatas dapat terlihat bahwa batas bawah pada indeks adalah 1 sedangkan batas atasnya n. Kemudian bisa dipisahkan menjadi dua sigma yang dijumlahkan. Yang pertama adalah memiliki batas bawah 1 dan batas atas m.
Sedangkan yang kedua memiliki batas bawah lanjutan berupa m+1 dengan batas atas berupa n. Dengan demikian maka batas indeks dan batas antara yang pertama dan yang kedua harus berurutan. Begitu juga jika dipisahkan menjadi tiga penjumlahan.
Contoh soalnya adalah seperti berikut:
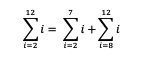
Anda bisa perhatikan notasi sigma diatas dan kita akan menjabarkannya menjadi penjumlahan seperti di bawah ini:
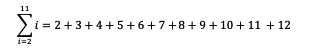
Setelah dijabarkan, selanjutnya bisa dibagi menjadi dua penjumlahan. Yaitu satu sigma dengan indeks 2 sampai 7 dan yang kedua adalah sigma dengan indeks 8 sampai 12. Adapun penjabarannya adalah seperti berikut:

Bisa juga dengan dipisahkan antara suku pertama dan terakhir
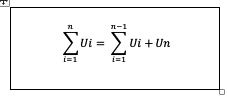
Sifat ini sangat berbeda dengan pemisahan yang telah dijelaskan sebelumnya, karena dalam notasi sigma tersebut yang dipisahkan adalah suku terakhirnya atau Un. Untuk lebih jelasnya, silakan simak contoh perhitungannya di bawah ini:
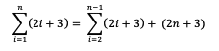
Anda bisa fokus dulu pada ruas sebelah kiri, yang kalau dijabarkan maka akan menjadi seperti berikut:

Dari penjabaran diatas maka dapat diketahui bahwa suku terakhir dalam penjumlahan tersebut adalah (2n + 3). Jika sudah mengerti sampai disini, maka sekarang bisa kita masukkan suku terakhir tersebut dalam bentuk penjumlahan. Hasilnya akan seperti ini:
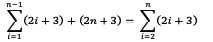
Contoh Soal Notasi Sigma
Agar lebih mudah dalam memahami pembahasan tentang materi kali ini, Anda bisa langsung menyimak beberapa contoh soal di bawah ini:
1. Hitunglah hasil dari penjumlahan di bawah ini
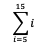
Soal diatas meminta Anda untuk menjumlahkan seluruh i yang dimulai dari i=5 sampai 15. Berikut ini pembahasan dan cara mengerjakannya.
Diketahui:
n atau batas atas adalah 15
i atau batas bawah adalah 5
formulanya adalah i
Jawaban:
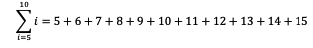
= 110
2.Berapakah hasil dari penjumlahan berikut?
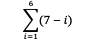
Pada soal tersebut Anda diminta untuk mencari jumlah semua (7 – i) yang dimulai dari batas bawah yaitu 1 dan sampai batas atas yaitu 6. Berikut ini pembahasannya.
Diketahui:
n atau batas atas = 6
i atau indeks batas bawah = 1
formula = 7 – i
Jawaban:
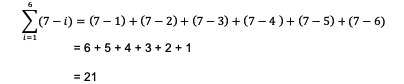
3. Tentukan berapa hasil notasi sigma berikut:
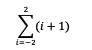
Pada soal diatas, Anda diminta untuk menjumlahkan semua (i+1) yang dimulai dari batas bawah yaitu i=-2 serta batas atas yaitu 2. Berikut ini pembahasannya:
Diketahui:
n atau batas atas sigma = 2
i atau batas bawah = -2
formula = i + 1
Jawaban:

= – 1 + 0 + 1 + 2 + 3
= 5
4. Berapakah hasil dari penjumlahan berikut:
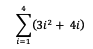
Berdasarkan soal tersebut maka bisa dijabarkan seperti di bawah ini:

Selanjutnya bisa dijabarkan lagi menjadi seperti berikut:

= 3 (12 + 22 + 32 + 42) + 4 (1 + 2 + 3 + 4)
= 3 (30) + 4 (10)
= 310
Pada dasarnya materi mengenai notasi sigma harus dipahami dengan baik karena sering digunakan untuk mendukung materi lainnya seperti deret, barisan maupun induksi matematika. Apalagi fungsi utama dari perhitungan ini adalah untuk meringkas penjumlahan sehingga tidak terlalu panjang.
Baca Juga: