Simpangan baku adalah konsep penting dalam statistika yang digunakan untuk mengukur sejauh mana data tersebar di sekitar nilai rata-rata. Istilah ini juga disebut dengan standar deviasi. Dalam analisis data, sering kali ingin mengetahui seberapa variabel atau data menyebar dari nilai tengahnya.

Dalam panduan ini, akan dibahas secara lengkap mengenai standar deviasi, termasuk definisi dan pengertian standar deviasi, rumus perhitungannya, serta contoh penggunaannya dalam analisis data.

Kamu akan belajar bagaimana menghitung standar deviasi untuk data tunggal maupun data kelompok, serta memahami arti dari nilai standar deviasi dalam interpretasi data.

Daftar Isi

Apa Itu Simpangan Baku?

Standar deviasi didefinisikan sebagai nilai statistik yang digunakan untuk mengukur sebaran data dalam sampel serta seberapa dekat lokasi titik data individu dengan rata-rata atau mean nilai dari sampel tersebut. Konsep ini digunakan untuk memberikan informasi tentang sejauh mana data tersebar dari nilai rata-rata.

Semakin tinggi standar deviasi, semakin besar variasi atau perbedaan antara titik data individu dengan rata-rata kamu. Nilai standar deviasi pada kumpulan data dapat bernilai nol atau lebih kecil dari angka nol.

Jika nilainya nol, maka seluruh nilai dalam suatu himpunan data tersebut memiliki nilai yang sama. Namun, jika nilai dari simpangan baku atau standar deviasi lebih kecil atau lebih besar dari titik nol, itu menandakan titik data individu terletak lebih jauh dari nilai rata-rata.

Untuk menghitung nilai standar deviasi pada kumpulan data, kamu perlu mengikuti beberapa langkah. Pertama, hitunglah nilai rata-rata (mean) dari seluruh titik data. Selanjutnya, hitung variansi data dengan cara mengambil selisih setiap titik data dari nilai rata-rata.

Kemudian kuadratkan nilai simpangan di setiap titik data, dan selisihkan dengan kuadrat dari nilai rata-ratanya. Nilai ini disebut sebagai variansi. Setelah kamu mendapatkan nilai variansi, langkah berikutnya adalah mengakar kuadratkan nilai variansinya untuk mendapatkan nilai standar deviasi.

Dengan begitu, kamu akan mendapatkan informasi tentang seberapa dekat atau jauh titik data individu dari nilai rata-rata dalam kumpulan data tersebut.

Apakah Simpangan Baku Sama dengan Simpangan Rata-rata?

Dalam dunia statistika, terdapat dua konsep penting yang sering digunakan untuk mengukur sebaran data, yaitu standar deviasi dan simpangan rata-rata. Kedua konsep ini memiliki perbedaan yang perlu dipahami dengan baik.

1. Simpangan Rata-rata

Simpangan rata-rata adalah konsep menggambarkan seberapa jauh titik data individu dari nilai rata-rata pada sekelompok data. Semakin kecil simpangan rata-rata, semakin dekat titik data dengan nilai rata-rata, menunjukkan bahwa data cenderung lebih homogen.

Konsep ini berguna untuk mengetahui sejauh mana data-data tersebut menyimpang dari nilai pusatnya.

2. Standar Deviasi

Di sisi lain, standar deviasi digunakan untuk mengukur sebaran data dalam sampel dan seberapa besar variasi atau perbedaan antara titik data individu dengan rata-rata. Semakin tinggi standar deviasi, semakin besar variasi data, dan semakin jauh titik data individu dari rata-rata.

Kedua konsep ini penting dalam menganalisis data dan memberikan informasi tentang variasi data dalam sampel. Namun, mereka memiliki rumus dan penggunaan yang berbeda-beda, jadi penting untuk memahami perbedaan antara standar deviasi dan simpangan rata-rata dengan baik.

Dengan pemahaman yang tepat, kamu dapat menggunakan kedua konsep ini secara efektif dalam analisis statistikmu.

Fungsi Simpangan Baku

Beberapa fungsi dari standar deviasi adalah:

1. Mengukur sebaran data

Standar deviasi digunakan untuk menilai sejauh mana data tersebar dari nilai rata-rata. Semakin tinggi standar deviasi, semakin besar variasi atau perbedaan antara titik data individu dengan nilai rata-rata.

2. Menentukan homogenitas data

Kamu dapat menggunakan standar deviasi untuk menilai homogenitas atau keseragaman data dalam sebuah kelompok. Jika standar deviasi mendekati nol, maka data cenderung homogen atau memiliki sedikit variasi.

Sebaliknya, jika standar deviasi besar, maka data cenderung heterogen atau memiliki variasi yang lebih besar.

3. Mengidentifikasi outlier

Simpangan baku fungsinya untuk membantu kamu mengenali adanya outlier atau titik data yang jauh dari nilai rata-rata. Jika terdapat titik data dengan standar deviasi yang signifikan, maka titik tersebut dapat dianggap sebagai outlier yang perlu kamu perhatikan secara khusus.

4. Mengukur risiko

Standar deviasi juga berguna untuk mengukur risiko atau variasi hasil investasi. Dalam konteks pengelolaan dana investor bagi startup, standar deviasi membantu kamu memahami sejauh mana hasil investasi dapat bervariasi dari rata-rata yang diharapkan.

Rumus Simpangan Baku

Berikut ini adalah rumus dari standar deviasi.

1. Sampel

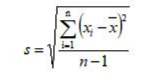
Keterangan:

xi adalah nilai dari masing-masing titik data dalam sampel.
x̄ adalah nilai rata-rata dari seluruh data dalam sampel.
n adalah jumlah data dalam sampel.
√ adalah simbol untuk akar kuadrat.
Σ adalah simbol untuk menjumlahkan seluruh nilai di dalam kurung.
(n – 1) merupakan faktor koreksi yang digunakan karena kita menggunakan sampel data, bukan seluruh populasi. Faktor koreksi ini digunakan untuk mendapatkan estimasi yang lebih akurat dari standar deviasi populasi.

2. Populasi

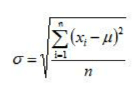
Keterangan:

xi adalah masing-masing nilai dalam populasi data.
μ adalah nilai rata-rata (mean) dari populasi data.
N adalah jumlah total data yang ada dalam populasi.
√ adalah simbol untuk tanda akar kuadrat.
Σ adalah simbol untuk menjumlahkan semua nilai di dalam kurung.

Perbedaan utama antara rumus standar deviasi populasi dan standar deviasi sampel terletak pada penyebutnya. Pada rumus standar deviasi populasi, penyebutnya adalah jumlah total data dalam populasi (N).

Sedangkan pada rumus simpangan baku sampel, penyebutnya adalah jumlah total data dalam sampel dikurangi satu (n-1). Faktor koreksi (n-1) pada rumus standar deviasi sampel digunakan untuk memberikan estimasi yang lebih akurat.

Ini karena sampel cenderung memiliki variabilitas lebih besar daripada keseluruhan populasi. Sedangkan pada populasi keseluruhan, tidak ada faktor koreksi yang diperlukan karena seluruh data sudah termasuk dalam perhitungan.

3. Varian

Rumus varian data adalah:

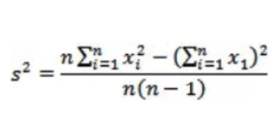
Rumus ini bisa digunakan sebagai cara mencari simpangan baku, yaitu dengan cara s = √varian. Ini bisa menjadi alternatif yang dapat kamu lakukan dalam menyelesaikan soal terkait standar deviasi.

Contoh Soal Simpangan Baku

Berikut adalah contoh soal yang dapat menambah pemahamanmu mengenai materi standar deviasi. Kamu dapat mencoba untuk menyelesaikannya terlebih dahulu sebelum melihat pembahasannya.

1. Soal: Hitunglah standar deviasi dari data kelompok berikut:

Kelas	Frekuensi
10 – 20	5
20 – 30	10
30 – 40	15
40 – 50	20

Jawaban:

Menghitung titik tengah kelas:

Titik tengah kelas 10-20: (10 + 20) / 2 = 15 Titik tengah kelas 20-30: (20 + 30) / 2 = 25 Titik tengah kelas 30-40: (30 + 40) / 2 = 35 Titik tengah kelas 40-50: (40 + 50) / 2 = 45

Menghitung rata-rata:

Rata-rata (μ) = ((15 × 5) + (25 × 10) + (35 × 15) + (45 × 20)) / (5 + 10 + 15 + 20) Rata-rata (μ) = (75 + 250 + 525 + 900) / 50 Rata-rata (μ) = 1750 / 50 Rata-rata (μ) = 35

Menghitung varians:

Varians = (((15-35)^2 * 5) + ((25-35)^2 * 10) + ((35-35)^2 * 15) + ((45-35)^2 * 20)) / 50 Varians = ((400 * 5) + (100 * 10) + (0 * 15) + (100 * 20)) / 50 Varians = (2000 + 1000 + 0 + 2000) / 50 Varians = 5000 / 50 Varians = 100

Menghitung standar deviasi:

S = √Varians

S = √100

S = 10.52 (diambil dua angka di belakang koma)

Jadi, standar deviasi dari data kelompok tersebut adalah sekitar 10.52.

2. Soal: Seorang guru ingin mengetahui seberapa jauh nilai ujian matematika siswanya dari nilai rata-rata kelas. Nilai rata-rata kelas adalah 75 dan nilai siswa-siswanya adalah sebagai berikut: 80, 70, 85, 90, 60. Kamu diminta untuk menghitung standar deviasi dari data tersebut.

Penyelesaian:

Hitung rata-rata: (80 + 70 + 85 + 90 + 60) / 5 = 77
Hitung selisih antara setiap nilai dengan rata-rata: (80 – 77), (70 – 77), (85 – 77), (90 – 77), (60 – 77) = 3, -7, 8, 13, -17
Kuadratkan setiap selisih: 3^2, (-7)^2, 8^2, 13^2, (-17)^2 = 9, 49, 64, 169, 289
Jumlahkan semua hasil kuadrat tersebut: 9 + 49 + 64 + 169 + 289 = 580
Bagi hasil penjumlahan dengan jumlah data: 580 / 5 = 116
Ambil akar kuadrat dari hasil pembagian tersebut: akar(116) ≈ 10.77

Jadi, standar deviasi dari data tersebut adalah sekitar 10.77.

Soal: Sebuah perusahaan ingin mengetahui seberapa tersebar gaji karyawannya. Berikut adalah data gaji karyawan per bulan: 3 juta, 4 juta, 5 juta, 6 juta, 7 juta, 8 juta, 9 juta, 10 juta. Kamu diminta untuk menghitung standar deviasi dari data tersebut.

Penyelesaian:

Hitung rata-rata: (3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) / 8 = 6.125 juta
Hitung selisih antara setiap nilai dengan rata-rata: 3 – 6.125, 4 – 6.125, 5 – 6.125, 6 – 6.125, 7 – 6.125, 8 – 6.125, 9 – 6.125, 10 – 6.125 = -3.125, -2.125, -1.125, -0.125, 0.875, 1.875, 2.875, 3.875
Kuadratkan setiap selisih: (-3.125)^2, (-2.125)^2, (-1.125)^2, (-0.125)^2, 0.875^2, 1.875^2, 2.875^2, 3.875^2 = 9.766, 4.516, 1.266, 0.016, 0.766, 3.516, 8.016, 15.016
Jumlahkan semua hasil kuadrat tersebut: 9.766 + 4.516 + 1.266 + 0.016 + 0.766 + 3.516 + 8.016 + 15.016 = 43.92
Bagi hasil penjumlahan dengan jumlah data: 43.92 / 8 = 5.49
Ambil akar kuadrat dari hasil pembagian tersebut: akar(5.49) ≈ 2.34

Jadi, standar deviasi dari data tersebut adalah sekitar 2.34 juta.

Penutup

Contoh soal di atas dapat membantu kamu dalam memahami standar deviasi dan implementasinya dalam kehidupan sehari-hari. Kamu dapat mengulang pembahasan jika masih bingung dan mencoba untuk memahaminya kembali.

Simpangan baku merupakan salah satu konsep matematika yang perlu untuk dipahami dengan baik. Pemahaman konsep dan mengetahui rumus yang tepat adalah kunci untuk menyelesaikan soal. Kamu dapat terus berlatih dengan contoh soal agar dapat lebih memahami materi.

Baca Juga: