Barisan aritmatika merupakan salah satu ilmu dalam matematika yang memakai pola bilangan. Pola bilangan ini dapat berupa penjumlahan atau pengurangan tergantung bentuk soalnya. Tidak hanya barisan, ternyata juga terdapat deret aritmatika.
Deret aritmatika itu sendiri merupakan jumlah n suku pertama dari barisan aritmatika, yang berfungsi untuk menentukan jumlah bilangan di dalamnya. Pada umumnya, dalam soal barisan seperti ini akan ada beberapa bilangan dengan pola tertentu.
Contoh sederhananya dalam kehidupan sehari-hari adalah jumlah kenaikan gaji yang diterima setiap bulan. Misalnya pada bulan pertama didapat gaji 5000, bulan kedua menjadi 7000 dan bulan ketiga menjadi 9000, atau mengalami selisih kenaikan secara konstan.
Apa Itu Barisan Aritmatika?

Barisan aritmatika atau Un merupakan barisan yang terdiri atas bilangan dengan pola yang tetap. Pola bilangan ini saat disederhanakan akan membentuk operasi penjumlahan atau pengurangan. Masing-masing bilangan tersebut mempunyai selisih atau beda yang sama.
Selisih atau beda ini disimbolkan dengan b yang dapat dihitung dengan menjumlahkan atau mengurangi dua bilangan pada suku yang berdekatan, misalnya U3 – U3.
Apabila nilai beda atau b adalah positif, maka barisan tersebut mempunyai selisih yang tetap. Sedangkan nilai b negatif menunjukkan bahwa barisan ini mempunyai pola menurun.
Rumus
Rumus dasar dari barisan tersebut dapat kamu lihat berikut ini.
U1 = a (merupakan bilangan pertama dari barisan yang dilambangkan dengan a)
U2 = U1 + b atau a + b (dengan b adalah beda atau selisih dari suku bilangan yang berdekatan)
Maka dapat dirumuskan bahwa untuk mencari nilai suatu bilangan pada suku tertentu menggunakan rumus:
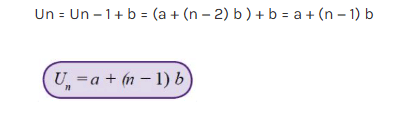
Barisan bilangan ini nantinya berkaitan dengan deret aritmatika yang menyatakan jumlah seluruh bilangan pada barisan tersebut. Kamu tidak perlu lagi menjumlahkan setiap bilangannya satu per satu, tapi cukup dengan memakai rumus deret aritmatika yang lebih memudahkan.
Sejarah Barisan Aritmatika
Aritmatika berasal dari bahasa Yunani yaitu arithmos yang berarti angka atau ilmu matematika yang mempelajrai tentang operasi dasar bilangan. Bagi orang awam, aritmatika sering dianggap sebagai sinonim atau persamaan kata dari bilangan.
Teori tentang angka inilah yang nantinya dapat menentukan bilangan yang dimaksud dalam sebuah perhitungan matematika. Prasejarah aritmatika dimulai saat ditemukannya sejumlah artefak yang menunjukkan penjumlahan dan pengurangan yang terkenal di dunia adalah Ishango dari Afrika Tengah.
Perhitungan ini sudah ada sejak 20.000 sampai 18.000 SM meskipun susah membuat intrepertasinya. Kemudian kisah tertulis yang menunjukka Mesir dan Babilonia dengan proses aritmatika dasar sudah ada sejak tahun 2000 SM.
Artefak yang menjelaskan hal tersebut mengungkapkan bahwa pemecahan masalah dengan karakteristik angka tertentu mempengaruhi kompleksitas suatu metode. Hal ini juga berhubungan dengan sistem hiegrolif atau angka Mesir dan angka Romawi yang menjadi tanda awal munculnya perhitungan.
Perkembangan aritmatika berlanjut dari aritmatika modern sampai peradaban Helenistik dari Yunani Kuno. Kemudian disusul dengan perhitungan Phytagoras yang juga menjadi pengantar aritmatika. Berbagai jenis perhitungan pun makin digunakan secara luas begitu juga dengan menghitung barisan aritmatika.
Operasi di Dalam Aritmatika
Operasi yang ada dalam ilmu aritmatika adalah penjulahan, pengurangan, perkalian, dan pembagian. Meskipun demikian, pelajaran dalam ilmu tersebut lebih mengutaman operasi yang lebih maju seperti manipulasi persentase, akar kuadrat, logaritma, eksponen dan fungsi trigonometri.
Ekpresi aritmatika harus sesuai dan sama dengan operasi yang sedang dimaksud. Ada beberapa metode yang paling umum digunakan, seperti notasi infix, penggunaan tanda kurung, notasi awalan satau postfix, kemudian memperbaiki urutan bilangan dengan urutan ekseskusi.
Kumpulan objek yang ada dalam aritmatika kecuali pembagian dengan nol dapat dilakukan secara langsung asalkan mematuhi hukum distribusi yang disebut dengan bidang. Untuk itu, dalam penyelesaiannya terdapat teori aritmatika seperti di bawah ini.
1. Teori Aritmatika Dasar
Teori dasar dalam ilmu aritmatika ini menyatakan bahwa bilangan bulat dengan jumlahnya lebih dari satu mempunyai faktorisasi prima yang unik atau tidak biasa. Artinya representasi bilangannya sebagai hasil kali faktor prima dan tidak termasuk urutan faktor.
Contohnya angka 252 yang hanya mempunyai satu faktorisasi prima yaitu 22 x 32 x 71. Elemen ekuides pertama kali memperkenalkan teori ini dan memberikan bukti secara parsial atau disebut dengan lemma Ekuides oleh Carl Friedrich Gauss.
2. Teori Bilangan
Teori bilangan merupakan sinonim dari aritmatika itu sendiri yang ditemukan pada abad ke-19. Teori ini menangani masalah yang berhubungan dengan operasi dasar seperti primality dan terbagi menjadi solusi persamaan bilangan bulat (teorema Fermat).
Selain itu juga berhubungan dengan teori bilangan seperti teori bilangan analitik, aljabar, gemoteri aljabar aritmatika dan geometri diofantin. Teori tersebut dibuktikan dengan Wiles yang menyatakan metode canggih dapat melampaui metode aritmatika klasih untuk memecahkan perhitungan aritmatika.
Perbedaan Deret dan Barisan Aritmatika
Selain barisan, pola bilangan dalam bidang aritmatika juga ada yang disebut dengan deret. Deret aritmatika merupakan penjumlahan antar suku-suku yang ada dalam barisan tersebut. Untuk penjumlahannya dimulai dari suku pertama hingga suku ke-n barisan yang dilambangkan dengan Sn.
Rumus menghitung deret aritmatika tersebut dapat dinyatakan dengan:
Jadi, dapat disimpulkan bahwa barisan dan deret mempunyai perbedaan dalam menyatakan bilangannya. Barisan berarti menyatakan pola bilangan yang mempunyai selisih sama sedangkan deret merupakan penjumlahan dari suku-suku yang ada dalam barisan tersebut.
Dalam hal ini, kamu harus tahu bilangan mana yang menjadi suku pertama atau U1 atau a dan juga selisih dari suku-suku bilangan yang disebut dengan beda (b). Apabila kedua bilangan tersebut sudah diketahui maka akan lebih mudah untuk menentukan bilangan suku ke-n dan jumlah dari bilangannya (deret).
Suku Bilangan Barisan Aritmatika
Suku bilangan dalam barisan ini dilambangkan dengan an atau Un yang diurutkan dengan cara menjumlahkan suku bilangan pertama dengan (n-1) dan dikali selisih atau beda bilangan tersebut. Pola perhitungan suku bilangan pada barisan ini dapat dibuat menjadi:
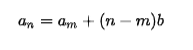
Agar lebih memahami suku bilangan ini, kamu harus mengetahui istilah berikut yang berhubungan dengan perhitungan artimatika. Dengan begitu, pemahaman tentang menggunakan rumus dan mengaplikasikannya akan lebih mudah dan gampang.
1. Suku Tengah
Suku tengah adalah suku yang berada tepat ditengah barisan aritmatika apabila jumlah bilangan yang ada adalah ganjil. Contohnya jika am dan an dinyatakan dengan m < n yang engapit sebanyak ganjil suku bilangan maka n – m dan n + m dalah bilangan genap, rumusnya adalah sebagai berikut.
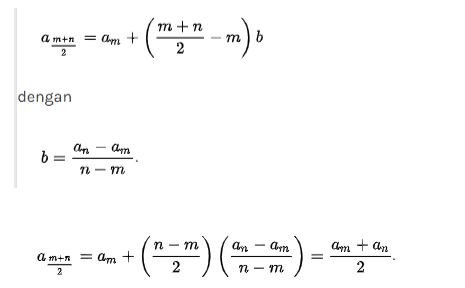
2. Beda
Seperti yang sudah dijelaskan sebelumnya bahwa beda adalah selisih di antara dua suku bilangan yang berdekatan dalam aritmatika. Agar tidak bingung lagi, cara mencari beda dalam barisan ini adalah sebagai berikut.
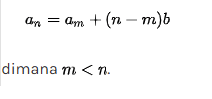
Penerapan Deret dan Barisan Aritmatika dalam Kehidupan
Dalam kehidupan barisan dan deret aritmatika ternyata mempunyai fungsi yang sangat baik untuk menghitung sesuatu. Berikut ini contoh kegiatan yang berhubungan dengan barisan dan deret aritmatika yang menjadi aplikasi di kehidupan sehari-hari.
1. Bidang Keuangan
Matematika keungan memakai konsep barisan dan deret untuk menentukan bunga pinjaman atau bunga tabungan nasabah. Jika seseorang menabung Rp1000 pada setiap akhir tahunnya, maka selama 5 tahun akan memperoleh bungan tahunan sebanyak 5%.
Sehingga jumlah akhir dari total tabungannya dihitung menggunakan deret aritmatika, yaitu nilai a adalah 1000 dan nilai bedanya adalah 50 (5% dari 1000). Setelah digunakan rumus Sn, maka didapatkan jumlah seluruh tabungan orang tersebut adalah 5250 setelah 5 tahun.
Tentunya hal ini sangat bermanfaat karena dapat mempercepat sistem perhitungan di dunia keuangan sehingga lebih mudah dalam menghitung jumlah uang. Apalagi dengan sistem bunga yang selalu konsisten dapat dijadikan sebagai selisih tabungan setiap tahunnya.
Jika kamu bekerja di bidang keuangan, maka rumus dan konsep barisan atau deret ini sudah harus melekat di otak karena selalu saja terpakai. Jadi, meskipun konsep tersebut hanya dipelajari di sekolah namun pemakaiannya sangat luas untuk berbagai bidang kehidupan.
2. Ilmu Fisika
Pada dasarnya, ilmu pengetahuan alam erat kaitannya dengan hitungan. Contohnya, setiap ilmu yang ada dalam dunia fisika selalu menggunakan rumus yang didasari oleh perhitungan matematika. Perhitungan matematika yang tidak kalah sering digunakan dalam fisika adalah barisan dan deret aritmatika.
Barisan dan deret ini digunakan untuk menghitung jarak, posisi, kecepatan suatu benda dalam periode waktu tertentu. Misalnya saat seseorang mengendarai mobil dengan kecepatan 70 km/jam dalam waktu 4 jam, maka untuk mengetahui jarak tempuhnya dapat memakai konsep deret aritmatika.
Jika melihat dari rumusnya, Sn merupakan total jarak yang ditempuh orang tersebut, kemudian n adalah jumlah waktu yang dihabiskan, dan U1 atau suku pertama adalah kecepatan ia mengendarai mobil. Kemudian untuk beda atau selisihnya dapat dinyatakan nol karena selalu konstan.
Setelah dilakukan perhitungan akan didapatkan jarak tempuhnya sejauh 240 km. Dengan begitu, jika kamu lupa dengan rumus kecepatan yang ada dalam ilmu fisika, kamu dapat memakai konsep barisan dan deret ini sehingga perhitungannya jadi lebih mudah.
3. Bahasa Pemograman
Deret dan barisan ini juga dipakai dalam bahasa pemograman untuk melakukan operasi penjumlahan bilangan yang selisihnya sama. Contohnya adalah ketika kamu ingin menghitung rata-rata dari 10 bilangan bulat berurutan, maka dapat dihitung memakai konsep deret aritmatika.
Nilai U1-nya adalah 1 dan bedanya juga satu, kemudian didapatkan nilai Un-nya adalah bilangan terakhir yaitu 10. Selanjutnya cari rata-rata bilangan dengan menjumlahkan bilangan pertama dan bilangan terakhir, nantinya akan didapatkan nilai 5,5.
Kemudian pemakaian barisan dan deret ini juga berguna dalam memecahkan berbagai macam kode pemograman. Hal ini disebabkan oleh ilmu dasar pemograman adalah hitungan matematika yang nantinya menghasilkan rumus tertentu.
Apabila kamu bekerja atau terjun di bidang pemograman, tentunya barisan dan deret aritmatika akan terus terpakai dan menjadi dasar utama sebelum melanjutkan ke pendalaman ilmunya.
Ilmu barisan aritmatika tentunya dipelajari ketika kamu masih di masa sekolah yang bertujuan untuk menghitung dan menentukan suku suatu bilangan. Kemudian dikaitkan langsung dengan deret aritmatika yang dapat menjumlahkan seluruh bilangan yang ada dalam barisan tersebut dengan cepat.
Selain itu, ilmu perhitungan ini juga digunakan dalam bidang ilmu lainnya seperti keuangan, ilmu fisika bahkan untuk memecahkan kode pemograman. Oleh karena itu, mempelajari materi barisan dan deret aritmatika sangat berguna bagi kehidupan dan berbagai cabang ilmu lainnya.
Baca Juga: