Simpangan kuartil adalah salah satu konsep statistik yang sangat penting dalam analisis data. Istilah ini sering digunakan dalam bidang statistika untuk mengukur tingkat variabilitas atau penyebaran data dalam suatu himpunan nilai.
Konsep ini juga disebut dengan jangkauan semi antar kuartil atau deviasi kuartil. Jangkauan semi antar kuartil ini memungkinkan kamu untuk memahami bagaimana data tersebar secara lebih mendalam, terutama ketika kamu memiliki data yang berbentuk kelompok atau berkelompok.
Dalam pembahasan ini, kamu akan menjelaskan dengan jelas dan sederhana apa itu deviasi kuartil, bagaimana cara menghitungnya, dan apa interpretasi dari nilai dari deviasi kuartil tersebut.
Apa Itu Simpangan Kuartil?
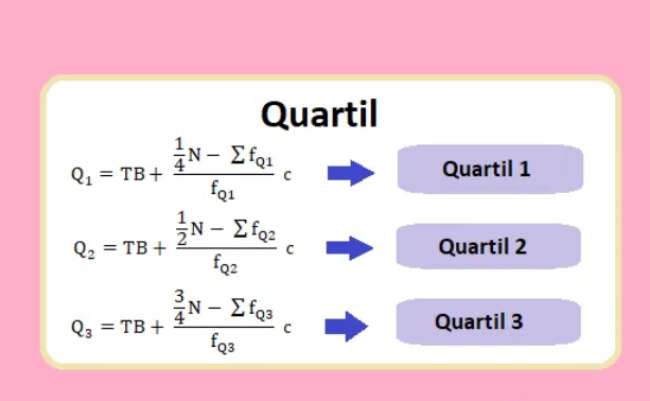
Kuartil adalah istilah yang digunakan untuk mempartisi data berurutan menjadi empat bagian yang memiliki jumlah data yang sama pada setiap bagiannya. Dalam analisis statistik, terdapat tiga nilai kuartil, yaitu kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3).
Jangkauan semi antar kuartil sendiri adalah selisih antara nilai kuartil atas (Q3) dengan nilai kuartil bawah (Q1). Untuk menghitung deviasi kuartil, kamu perlu menentukan nilai Q3 dan Q1 terlebih dahulu. Deviasi kuartil sebenarnya mewakili rata-rata jarak antara kuartil kedua (Q2) dengan kuartil pertama (Q1) atau kuartil ketiga (Q3).
Apa itu simpangan kuartil atas? Deviasi kuartil atas dihitung sebagai setengah dari jangkauan antar kuartil yang diukur dari nilai kuartil atas (Q₃) ke nilai tertinggi dalam data.
Sementara itu, jangkauan antar kuartil bawah dihitung sebagai setengah dari jangkauan antar kuartil yang diukur dari nilai terendah dalam data ke nilai kuartil bawah (Q₁).
Selain itu, terdapat ukuran statistik lain yang dikenal dengan nama simpangan baku atau simpangan standar (standard deviation). Simpangan baku adalah simpangan digunakan untuk menggambarkan sejauh mana data tersebar di sekamur nilai rata-rata.
Cara menghitung simpangan baku adalah dengan mengukur jarak penyimpangan setiap titik data dari nilai rata-rata, lalu diambil rata-rata dari jarak-jarak tersebut.
Ketiga ukuran tersebut, yaitu jangkauan semi antar kuartil atas, simpangan kuartil bawah, dan simpangan baku, memiliki peran yang berbeda dalam menganalisis data dan memberikan gambaran tentang penyebaran data serta tingkat variasi yang ada dalam data tersebut.
Penggunaan ukuran-ukuran ini membantu dalam memberikan pemahaman yang lebih komprehensif tentang karakteristik data dan mempermudah dalam mengambil kesimpulan dalam analisis statistik.
Apa Fungsi Simpangan Kuartil?

Jangkauan semi antar kuartil memiliki berbagai fungsi dalam analisis data, di antaranya:
1. Mengukur Penyebaran Data
Jangkauan semi antar kuartil digunakan untuk menilai sejauh mana data tersebar di sekamur nilai kuartil. Semakin besar deviasi kuartil, semakin besar juga penyebaran data.
2. Mendeteksi Pencilan (Outlier)
Pencilan adalah data yang jauh dari nilai rata-rata atau nilai kuartil. Jangkauan antar kuartil berperan penting dalam mengidentifikasi keberadaan pencilan pada data. Jika terdapat data yang berjarak jauh dari jangkauan antar kuartil, data tersebut dapat dianggap sebagai pencilan.
3. Membandingkan Penyebaran Data Antar Kelompok
Deviasi kuartil digunakan untuk membandingkan penyebaran data antar kelompok. Jika deviasi kuartil pada kelompok A lebih besar daripada kelompok B, dapat disimpulkan bahwa data pada kelompok A lebih tersebar daripada kelompok B.
4. Menentukan Batas Nilai yang Normal
Selanjutnya, fungsi simpangan kuartil adalah untuk membantu menentukan batas nilai yang normal pada suatu data. Batas nilai normal dapat dihitung dengan mengambil nilai kuartil bawah (Q₁) dikurangi 1,5 kali deviasi kuartil, dan nilai kuartil atas (Q₃) ditambah 1,5 kali deviasi kuartil.
Data yang berada di luar batas nilai normal dapat dianggap sebagai data yang tidak normal atau pencilan.
Dengan memahami berbagai fungsi deviasi kuartil, kamu dapat mengaplikasikannya dalam analisis data untuk mendapatkan informasi yang lebih mendalam mengenai penyebaran dan karakteristik data yang dimiliki.
Rumus Simpangan Kuartil
Sebelum kamu melanjutkan untuk memahami rumus-rumusnya, perlu untuk memahami perbedaan antara data tunggal dan data kelompok terlebih dahulu. Data tunggal adalah data yang disajikan secara sederhana, tidak mengandung interval, dan jumlahnya tidak terlalu banyak.
Sementara itu, data kelompok adalah data yang telah dikelompokkan dalam bentuk interval. Contohnya, data dapat dikelompokkan menjadi rentang 1 sampai 5, 6 sampai 10, dan seterusnya. Jumlah data pada jenis ini lebih banyak dan seringkali tersaji dalam tabel frekuensi.
1. Data Tunggal
Rumus deviasi kuartil pada data tunggal dan data kelompok memiliki perbedaan dalam cara menghitung nilai kuartil bawah (Q₁) dan kuartil atas (Q₃). Berikut adalah perbedaan rumus deviasi kuartil pada data tunggal dan data kelompok.
Pertama, data diurutkan secara berurutan. Nilai kuartil bawah (Q₁) didapatkan dari nilai data pada posisi ke-n/4, dan nilai kuartil atas (Q₃) didapatkan dari nilai data pada posisi ke-3n/4, di mana n adalah jumlah data.
Setelah itu, deviasi kuartil dapat dihitung menggunakan rumus Simpangan Kuartil (Qd) = ½ (Q₃ – Q₁)
2. Data Kelompok
Langkah awal adalah menentukan kelas frekuensi untuk data kelompok. Nilai kuartil bawah (Q₁) diperoleh dari nilai data pada batas kelas bawah dari kelas tempat median berada, dan nilai kuartil atas (Q₃) diperoleh dari nilai data pada batas kelas atas dari kelas tempat median berada. Selanjutnya, deviasi kuartil dapat dihitung menggunakan rumus Qd = ½ (Q₃ – Q₁)
Jadi, perbedaan rumus deviasi kuartil pada data tunggal dan data kelompok terletak pada cara mendapatkan nilai kuartil bawah (Q₁) dan kuartil atas (Q₃). Meskipun rumusnya sama, cara menghitung nilai kuartil bawah dan kuartil atas berbeda, tergantung pada tipe data yang kamu miliki.
Contoh Soal Simpangan Kuartil
Berikut adalah beberapa contoh soal yang dapat menambah pemahaman kamu mengenai deviasi kuartil.
Soal 1
Soal: Diberikan data tinggi badan siswa SMA sebagai berikut: 160, 165, 170, 155, 175, 162, 168, 160, 158, 172. Hitunglah deviasi kuartil dari data tersebut.
Pembahasan: Langkah pertama adalah mengurutkan data secara terurut dari yang terkecil hingga terbesar: 155, 158, 160, 160, 162, 165, 168, 170, 172, 175. Selanjutnya, tentukan kuartil bawah (Q₁) dan kuartil atas (Q₃).
Dalam kasus ini, karena terdapat 10 data, maka Q₁ berada pada posisi ke-3 (indeks ke-2) dan Q₃ berada pada posisi ke-8 (indeks ke-7). Q₁ = 160 Q₃ = 170 Setelah itu, hitunglah deviasi kuartil menggunakan rumus: Qd = (Q₃ – Q₁) / 2 = (170 – 160) / 2 = 5
Jadi, deviasi kuartil dari data tinggi badan siswa SMA tersebut adalah 5.
Soal 2
Soal: Berikut adalah tabel data jumlah penjualan produk dalam ribuan rupiah pada toko A selama 10 hari:
| Hari | Jumlah Penjualan |
| 1 | 50 |
| 2 | 60 |
| 3 | 55 |
| 4 | 70 |
| 5 | 65 |
| 6 | 75 |
| 7 | 80 |
| 8 | 85 |
| 9 | 90 |
| 10 | 95 |
Hitunglah deviasi kuartil dari data penjualan tersebut.
Pembahasan: Langkah pertama adalah mengurutkan data secara terurut dari yang terkecil hingga terbesar: 50, 55, 60, 65, 70, 75, 80, 85, 90, 95. Kemudian, tentukan kuartil bawah (Q₁) dan kuartil atas (Q₃).
Dalam kasus ini, karena terdapat 10 data, maka Q₁ berada pada posisi ke-3 (indeks ke-2) dan Q₃ berada pada posisi ke-8 (indeks ke-7). Q₁ = 60 Q₃ = 85 Selanjutnya, hitunglah deviasi kuartil menggunakan rumus: Qd = (Q₃ – Q₁) / 2 = (85 – 60) / 2 = 12.5
Jadi, deviasi kuartil dari data penjualan produk pada toko A adalah 12.5.
Soal 3
Soal: Sebuah toko buku mencatat penjualan buku selama 10 hari berturut-turut. Berikut adalah data penjualan buku dalam ribuan rupiah: 50, 60, 55, 70, 65, 75, 80, 85, 90, 95. Hitunglah deviasi kuartil dari data penjualan tersebut.
Pembahasan: Langkah pertama adalah mengurutkan data secara terurut dari yang terkecil hingga terbesar: 50, 55, 60, 65, 70, 75, 80, 85, 90, 95. Selanjutnya, tentukan kuartil bawah (Q₁) dan kuartil atas (Q₃).
Dalam kasus ini, karena terdapat 10 data, maka Q₁ berada pada posisi ke-3 (indeks ke-2) dan Q₃ berada pada posisi ke-8 (indeks ke-7). Q₁ = 60 Q₃ = 85
Setelah itu, gunakan rumus simpangan Kuartil (Qd) = ½ (Q₃ – Q₁) = ½ (85 – 60) = 12. Jadi, deviasi kuartil dari data penjualan buku selama 10 hari tersebut adalah 12.5 ribu rupiah.
Soal 4
Soal: Sebuah perusahaan mengadakan tes seleksi untuk calon karyawan. Data nilai tes seleksi tersebut dikelompokkan ke dalam beberapa kelas frekuensi dengan rentang nilai tertentu. Data tersebut adalah sebagai berikut:
| Kelas | Frekuensi Rentang Nilai |
| 1 | 50 – 59 |
| 2 | 60 – 69 |
| 3 | 70 – 79 |
| 4 | 80 – 89 |
| 5 | 90 – 100 |
Perusahaan ingin menghitung deviasi kuartil dari data nilai tes seleksi tersebut. Hitunglah deviasi kuartil dari tabel tersebut.
Pembahasan: Pertama-tama, perlu menghitung frekuensi tiap kelas. Setiap kelas memiliki frekuensi masing-masing, misalnya: Kelas 1: 4 Kelas 2: 6 Kelas 3: 8 Kelas 4: 10 Kelas 5: 12. Selanjutnya, tentukan nilai tengah tiap kelas.
Dalam konteks ini, nilai tengah setiap kelas dapat dihitung dengan cara menjumlahkan batas bawah dan batas atas dari rentang nilai kelas, lalu hasilnya dibagi dua. Contohnya: Kelas 1: (50 + 59) / 2 = 54.5 Kelas 2: (60 + 69) / 2 = 64.5 Kelas 3: (70 + 79) / 2 = 74.5 Kelas 4: (80 + 89) / 2 = 84.5 Kelas 5: (90 + 100) / 2 = 95
Setelah itu, hitung total frekuensi dari seluruh kelas. Total frekuensi pada contoh ini adalah 40. Tentukan kuartil bawah (Q₁) dan kuartil atas (Q₃).
Dalam kasus ini, karena terdapat 40 data, maka Q₁ berada pada posisi ke-10 (indeks ke-9) dan Q₃ berada pada posisi ke-30 (indeks ke-29). Q₁ = 64.5 Q₃ = 90. Terakhir, hitung deviasi kuartil menggunakan rumus: Qd = (Q₃ – Q₁) / 2 = (90 – 64.5) / 2 = 12.75
Jadi, deviasi kuartil dari data nilai tes seleksi calon karyawan tersebut adalah 12.75.
Penutup
Contoh soal simpangan kuartal ini dapat membantu kamu dalam memahami materi dengan baik. Kamu dapat terus berlatih agar pemahaman semakin baik. Pembahasan soal yang beragam tentunya akan membantu kamu dalam menyelesaikan ujian terkait materi ini.
Baca Juga:




