Mungkin banyak yang tidak menyadari bahwa nomor rumah, angka pada plat kendaraan dan sebagainya merupakan contoh pola bilangan. Bilangan berpola merupakan bagian dari materi pelajaran matematika, yang juga dapat ditemui dalam keseharian.
Contoh lainnya yaitu pada permainan billiard, dimana bola-bola disusun dalam suatu bangun segitiga dan membentuk suatu pola. Jika diperhatikan dengan teliti, susunan bola billiard tersebut berpola dengan jumlah 1,2,3,4 dan 5 bola dari baris atas ke bawah.
Contoh pola bilangan juga bisa ditemui pada pelajaran biologi, yaitu saat amuba berkembang biak dengan membelah diri. Setiap amuba akan membelah menjadi 2, kemudian membelah lagi dan seterusnya.
Apa yang Dimaksud Pola Bilangan?
Dari beberapa contoh yang digambarkan di atas, apa yang dimaksud dengan bilangan berpola itu? Secara bahasa, pola berarti susunan atau bentuk yang menetap, sedangkan pengertian bilangan adalah satuan jumlah yang dilambangkan dengan angka-angka.
Sehingga dapat disimpulkan bahwa pengertian pola bilangan adalah satuan jumlah yang dilambangkan dengan angka yang memiliki susunan tertentu. Bilangan berpola dapat juga diartikan sebagai deretan angka yang telah disertai dengan aturan tersendiri dalam pola penyusunannya.
Jenis Pola Bilangan dan Rumusnya
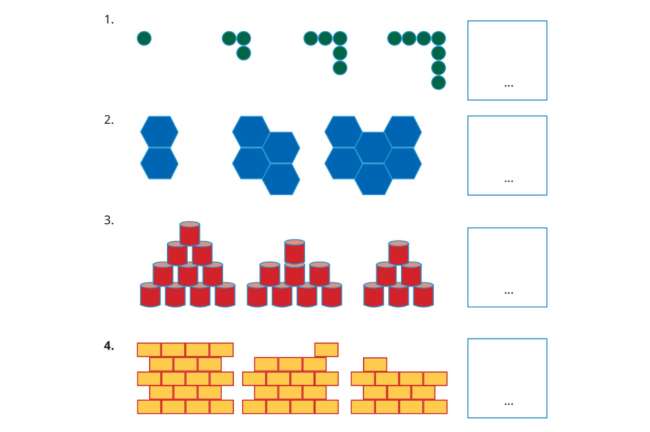
Bilangan berpola dibagi dalam beberapa jenis yang berbeda, dimana setiap macamnya memiliki rumus masing-masing. Agar lebih jelas, lihat jenis-jenis pola pada bilangan dan bagaimana rumus masing-masing berikut ini.
1. Bilangan Berpola Ganjil
Jenis yang pertama dan paling sering ditemui dalam kehidupan sehari-hari yaitu bilangan dengan pola ganjil. Pola ganjil dimulai dari angka 1 sampai dengan tidak terhingga, tapi syaratnya harus ganjil, tidak boleh genap dan lainnya.
- Rumus : Un = 2n-1
- Contoh : 1, 2, 3,…..,11, 13, 15, 17, 19, 21 dan seterusnya
Pada rumus tersebut “n “ merupakan urutan bilangan atau bilangan asli yang ingin dicari.
2. Bilangan Berpola Genap
Kalau ada bilangan dengan pola ganjil, maka sudah seharusnya ada juga yang genap. Pola terdiri dari bilangan genap yang habis dibagi 2 dan dimulai dari angka 2 hingga tidak terhingga.
- Rumus : Un = 2n
- Contoh : 2,4,6,….12,14,16,….,22,24,26, dan seterusya.
- Keterangan : n merupakan urutan bilangan
Jika diamati, pada bilangan berpola genap, semua angka-angka yang ditampilkan habis dibagi dengan 2.
3. Pola Aritmatika
Selanjutnya ada bilangan dengan pola aritmatika, dimana angka-angka yang menyusunnya selalu memiliki selisih yang tetap diantara suku-sukunya. Jadi, misalnya selisih antara angka urutan pertama dan kedua adalah 3, maka selisih angka pada urutan kedua dan ketiga juga sama dan seterusnya.
- Rumus : Un = a + (n-1)b
- Contoh : 4,8,12,16,20 dan seterusnya (selisih 4)
Keterangan rumusnya yaitu :
- a : suku pertama deret angka pada pola
- b : selisih suku angka
- n : urutan angka
Rumus pada pola aritmatika ini sangat membantu untuk menyelesaikan soal matematika tentang deret angka.
4. Bilangan Berpola Geometri
Jika pada bilangan dengan pola aritmatika, selisih antara dua suku dalam deret angka nilainya sama, agak berbeda denga pola geometri. Pengertian pola bilangan geometri yaitu susunan angka dimana rasio antara dua suku memiliki nilai yang selalu tetap.
- Rumus : Un = arn – 1
- Contoh : 3,12,48, 192 dan seterusnya
Dari rumus dan contoh di atas, keterangannya adalah sebagai berikut :
- a : suku pertama dari susunan angka
- r : rasio
- n : urutan bilangan
Contoh pada pola angka di atas memiliki rasio 4, dimana suku kedua adalah suku pertama yang dikalikan 4, suku ketiga adalah hasil suku kedua dikalikan 4 dan seterusnya.
5. Pola Persegi
Bilangan berpola persegi adalah bilangan yang memiliki pola seperti persegi dan dibentuk oleh kuadrat. Dikatakan dibentuk oleh kuadrat, karena jumlah deret di sisi samping dan atas pola jumlahnya sama.
Supaya lebih jelas, pola persegi pada bilangan dapat dilihat melalui gambar berikut :
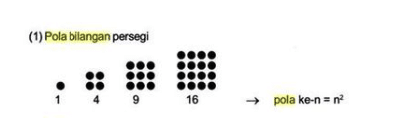
Rumus pola bilangan persegi yaitu Un = n2, seperti yang terlihat pada gambar. Jadi contoh bilangan dengan pola persegi yaitu 1, 4, 9, 16, 25, 36, 49 dan seterusnya.
6. Bilangan Berpola Persegi Panjang
Susunan atau pola pada bilangan bisa juga berbentuk seperti persegi panjang. Meskipun sekilas tampak tidak jauh berbeda dengan pola persegi, tapi rumus keduanya ternyata berbeda. Susunan angka-angka pada pola ini akan membentuk bangun datar persegi panjang.
Bagaimanakah gambaran pola persegi pada bilangan? Lihat contohnya di bawah ini.
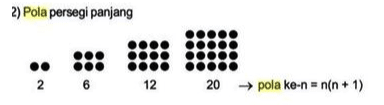
Bisa dibayangkan jika menggambar atau meletakkan benda-benda dengan susunan membentuk persegi panjang, maka itulah angka-angka yang akan didapatkan. Dari contoh gambar di atas didapatkan contoh pola persegi panjang pada bilangan yaitu 2,6, 12, 20 dan seterusnya.
Rumus bilangan dengan pola persegi panjang yaitu Un = n (n+1).
7. Bilangan Berpola Segitiga
Bentuk bangun datar lainnya yang bisa disusun menjadi pola pada bilangan adalah segitiga. Contoh yang mudah ditemui yaitu pada susunan bola billiard. Gambarannya bisa dilihat pada pola seperti di bawah ini.
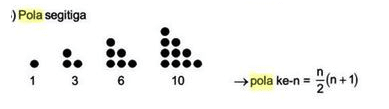
Dari susunan gambar di atas, didapatkan contoh bilangan berpola segitiga yaitu 1, 3, 6, 10 dan seterusnya. Rumus yang digunakan pada pola ini adalah Un = ½ n (n+1).
8. Pola Fibonacci
Apakah yang dimaksud pola fibonacci pada bilangan? Pola fibonacci adalah bilangan yang susunannya dimulai dari angka 0 dan 1. Suku angka selanjutnya diperoleh dari hasil penjumlahan dari dua suku kata yang berurutan.
Contohnya yaitu 0.1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3) dan seterusnya. Jadi, pola diawali dengan 0,1 kemudian 1 yang merupakan hasil penjumlahan 0 dan 1, lalu 1 ditambah 1 jadi 2, selanjutnya 1 ditambah dengan 2 yaitu 3 dan seterusnya.
Susunan bilangan berpola fibonacci dapat dilihat pada ilustrasi berikut ini.
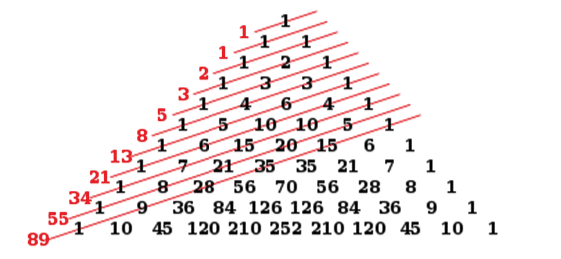
Rumus pola fibonacci bilangan yaitu Un = Un-1 + Un-2
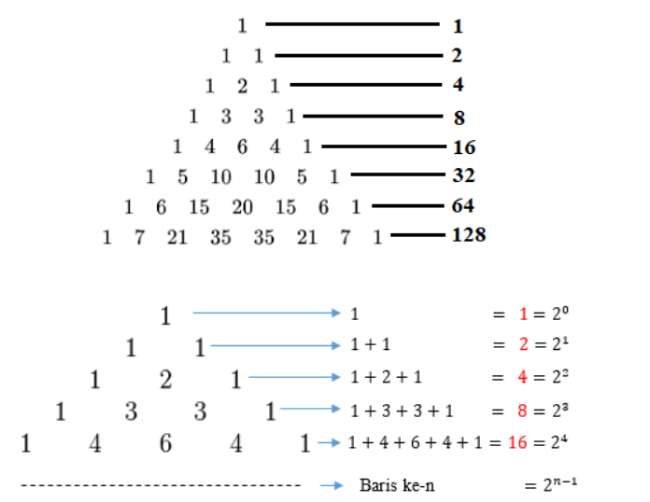
9. Pola Pascal
Masih ada satu lagi jenis pola pada bilangan yaitu pascal. Pengertian pola pascal pada bilangan tidak terlepas dari bentuk segitiga. Pascal adalah nama seorang ilmuwan bidang fisika yang berasal dari Perancis.
Temuannya dikenal sebagai segitiga pascal, yang juga bisa membentuk suatu pola pada bilangan. Ketentuan pola pascal pada bilangan adalah sebagai berikut :
- Baris teratas terdiri dari 1 kotak yaitu angka 1.
- Baris-baris selanjutnya yang ada pada segitiga pascal harus diawali angka 1 dan diakhiri dengan 1 juga.
- Jumlah pada kotak selanjutnya dituliskan hingga baris ke-2 sampai dengan baris tak terhingga (ke –n), yang didapatkan dari penjumlahan dua angka diagonal di atasnya.
- Setiap baris dalam segitiga bentuknya simetris.
- Banyaknya angka pada tiap baris merupakan kelipatan 2 dari jumlah bilangan yang terdapat pada baris sebelumnya.
Kalau masih bingung, silahkan perhatikan ilustrasi gambar segitiga pascal berikut ini.
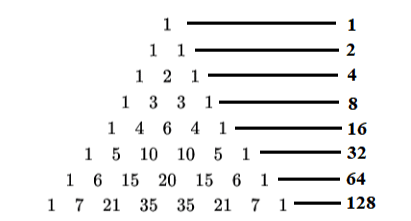
Rumus yang digunakan dalam pola pascal yaitu Un = 2n-1
Contoh Soal dan Pembahasannya
Jenis-jenis pola pada bilangan ada beberapa dan masing-masing memiliki rumus yang berbeda. Mencatat teori dan rumusnya saja belum cukup kalau tidak bisa menerapkannya dalam soal-soal. Untuk lebih memahami tentang pola bilangan, lihat beberapa contoh soal berikut.
1. Contoh Soal 1
Pada suatu deret angka dituliskan 1, 5, 25, 125, 625,…berapakah angka selanjutnya?
Pembahasan :
Perhatikan dulu berapa selisih antara kedua suku angka pada pola, yaitu 1, 5, 25, 125 dan 625 maka didapatkan rasio x 5. Jadi setiap suku angka selanjutnya merupakan hasil angka didepannya dikalikan 5.
Pada contoh dapat dilihat bahwa 5 adalah hasil 1×5, 25 didapatkan dari 5×5, 125 adalah 25×5 dan seterusnya. Jadi angka pada suku berikutnya adalah 625 x 5 yaitu 3125.
2. Contoh Soal 2
Suatu bilangan memiliki pola persegi panjang, berapakah angka yang ada di urutan ketujuh dan kedelapan?
Pembahasannya :
Untuk mengetahui berapa angka yang ada pada urutan ketujuh dan kedelapan pada bilangan berpola persegi panjang, lihat dulu bagaimana rumusnya. Rumus pola bilangan persegi panjang yaitu Un=n(n+1).
Setelah itu, masukkan angka ke dalam rumus tersebut, jika yang dicari adalah urutan ketujuh dan kedelapan, maka :
- U7 = 7 ( 7+1) = 7 x 8 = 56
- U8 = 8 (8+1) = 8 x 9 = 72
Dari perhitungan tersebut didapatkan hasil bahwa urutan ketujuh dan kedelapan pada pola persegi panjang adalah 56 dan 72.
3. Contoh Soal 3
Suatu susunan bilangan memiliki pola aritmatika dan dimulai dari angka 5 dan selisih antar suku adalah 2. Tuliskan deretan bilangannya dari urutan kedua hingga keenam.
Pembahasannya :
Cari dulu rumus untuk pola bilangan aritmatika, yaitu Un = a (n-1) b. Selanjutnya tinggal memasukkan angka ke dalam rumus tersebut, maka :
- U2 = 5 (2-1) x 2 = 5 x 2 = 10
- U3 = 5 (3-1) x 2 = 5 x 4 = 20
- U4 = 5 (4-1) x 2 = 5 x 6 = 30
- U5 = 5 (5-1) x 2 = 5 x 8 = 40
- U6 = 5 (6-1) x 2 = 5 x 10 = 50
Jadi didapatkan deretan angka aritmatika dengan susunan 5, 10, 20, 30, 40, 50.
4. Contoh Soal 4
Pada bilangan dengan pola segitiga, tuliskan susunannya, dari urutan kedua hingga kelima jika suku pertamanya adalah 10.
Pembahasannya :
Lihat dulu rumus bilangan dengan pola segitiga yaitu Un = ½ n (n+1). Lalu cari angka sesuai urutan yang inginkan, yaitu :
- U1 = ½ 1(1+1) = 1
- U2 = ½ 2(2+1) = 3
- U3 = ½ 3(3+1) = 6
- U4 = ½ 4(4+1) = 10
- U5 = ½ 5(5+1) = 15
Dari perhitungan menurut rumus, maka didapatkan susunan sebagai berikut 1, 3, 6, 10, 15.
Pola bilangan adalah angka-angka yang disusun berdasarkan pola tertentu. Bilangan berpola ada beberapa jenis dan masing-masing susunan memiliki rumus sendiri. rumus-rumus tersebut digunakan untuk mencari angka pada urutan tertentu.
Pola pada bilangan tidak hanya ada pada materi pelajaran matematika saja, tetapi juga diterapkan dalam berbagai hal di kehidupan. Contoh pola pada bilangan yang dapat ditemui dalam kehidupan sehari-hari, seperti nomor rumah, susunan bola billiard dan sebagainya.
Baca Juga: