Matematika adalah salah satu pelajaran yang sangat dekat dengan kehidupan sehari-hari. Dalam pelajaran ini adalah bahasan yang disebut dengan eksponen atau bilangan berpangkat. Bagaimana sifat-sifat eksponen ini bisa sampai dikenal?
Konon, metode ini pertama kali ditemukan oleh matematikawan bernama Euclid. Dia berasal dari Yunani yang juga dikenal sebagai bapak Geometri. Sedangkan penggunaan eksponen secara modern untuk pertama kalinya dilakukan pada tahun 1544 oleh Michael Stifel.
Bilangan eksponen ini menjadi metode yang banyak dipilih oleh para ahli atau peneliti. Khususnya ketika mereka harus menuliskan angka 0 dalam jumlah yang banyak ataupun bilangan desimal yang jumlahnya juga banyak di belakang angka 0 tersebut.
Pengertian Eksponen
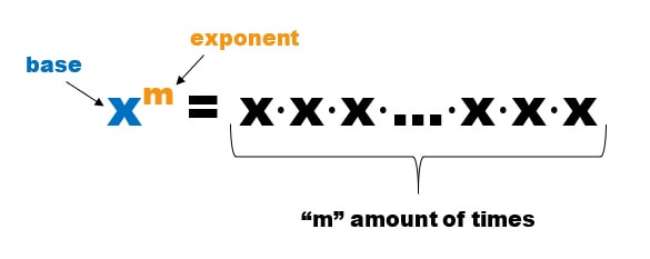
Eksponen itu merupakan metode perkalian yang diulang-ulang dengan metode yang sama. Maka dari itu, dalam eksponen ini ada bentuk an, di mana a merupakan basis sedangkan n merupakan pangkat atau eksponen.
Dengan kata lain, bilangan eksponen itu adalah bilangan berpangkat atau bilangan yang mengandung pangkat. Eksponen ini menjadi konsep ilmu Matematika dasar yang akan memberikan deskripsi tentang kekuatan suatu variabel atau angka.
Eksponen ini sendiri bisa berupa bilangan yang sifatnya negatif atau berupa bilangan desimal yang menyatakan pembagian dengan nilai pangkat yang sama dengan bilangan yang dimaksud.
Sifat-Sifat Eksponen Dan Contohnya
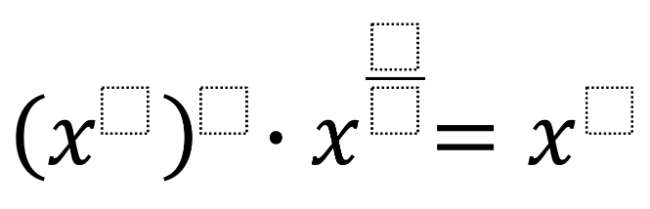
Kalau ditanya sifat-sifat eksponen ada berapa, jawabannya ada banyak, totalnya ada 8. Sifat-sifat ini biasa dipakai untuk menyelesaikan berbagai soal eksponen. Nah, sifat-sifat ini akan dijelaskan sesuai dengan kekuatannya.
Sebenarnya kalau dalam eksponen ada hukum dasar yang berlaku, yakni hukum pembagian dan hukum perkalian. Tetapi dua hukum ini kemudian dipecah sehingga sifat-sifat bilangan berpangkat atau eksponen menjadi seperti berikut ini.
1. Pengurangan
Sifat bilangan berpangkat pengurangan akan berlaku pada rumus pembagian. Pangkat bilangan akan dikurangi apabila dalam pembagian tersebut ada basis atau a yang sama. Makanya, rumus pengurangan akan ditulis seperti ini.
am : an = am-n
Mari ambil contoh soal sebagai berikut:
75 : 73 = 75-3= 72 =49
2. Penjumlahan
Sifat eksponen penjumlahan merupakan sifat yang berlaku dalam sebuah operasi hitung perkalian dengan basis atau a yang sama. Dalam operasi hitung perkalian ini, pangkatnya nanti akan ditambahkan sehingga penulisan rumusnya menjadi seperti ini.
am x an = a m + n
Mari ambil contoh soal sebagai berikut:
32 x 33 = 32+3 = 35 =243
3. Perkalian
Sifat-sifat bilangan eksponen ialah perkalian. Ini adalah sifat yang berlaku pada bilangan berpangkat yang juga dipangkatkan. Pangkat-pangkat ini kemudian akan dikalikan sehingga rumusnya menjadi seperti ini,
(am)n = am × n
Mari ambil contoh soal sebagai berikut:
(22)2 = 22×2 = 24 = 16
4. Perkalian pada Bilangan yang Juga Dipangkatkan
Apabila ada perkalian yang dipangkatkan, maka akan berlaku sifat eksponensial yang satu ini. Nantinya, masing-masing bilangan yang ada dalam perkalian tersebut akan dipangkatkan dengan pangkat yang dimaksud sehingga penulisan rumusnya menjadi seperti ini.
(a . b)m = am . bm
Mari ambil contoh soal sebagai berikut:
(2 x 4)2 = 22 x 32 = 4 x 14 = 56
5. Pangkat untuk Bilangan Pecahan
Pemberian pangkat juga bisa dilakukan pada bilangan pecahan. Kalau dalam bilangan pecahan seperti ini, maka antara pembilang dengan penyebut harus sama-sama diberi pangkat, tetapi dengan ketentuan b tidak sama dengan 0 atau b ≠ 0.
Dengan demikian, penyebut bilangan tersebut tidak boleh bernilai 0 dan untuk penulisan sifat eksponen yang satu ini sebagai berikut.
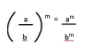
Mari ambil contoh soal sebagai berikut:
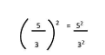
6. Pangkat Negatif
Sifat yang satu ini akan diterapkan pada bilangan eksponen yang mempunyai pangkat negatif. Cara menghitungnya ialah pangkat yang dimaksud bernilai 1 untuk setiap pangkat bilangan eksponen yang berubah sifat menjadi positif. Untuk rumusnya sebagai berikut:
a – n = 1an.
Mari ambil contoh soal sebagai berikut: 4 – 3 = 1.4.3
Tetapi ada penjelasan lain juga, di mana pangkat ini berlaku pada pecahan. Kalau seperti ini, apabila penyebut pecahan itu bernilai negatif, maka ketika dipindahkan ke atas akan berubah menjadi positif dan begitu pula sebaliknya. Sehingga rumusnya akan ditulis seperti ini.
1 / an = a-n
Untuk rumus yang satu ini, mari ambil contoh soal sebagai berikut:
1 / 35 = 3-5
7. Pangkat Pada Pecahan
Kalau dalam sifat yang satu ini, misalnya ada bilangan am dan diakarkan dengan n. Kalau bilangan ini kemudian diubah menjadi eksponen maka akar n tersebut akan berubah menjadi penyebut sedangkan pangkat m akan berubah menjadi pembilang.
Tetapi ini dengan catatan nilai n wajib lebih besar atau sama dengan 2. Untuk rumusnya seperti ini.
n√am = am/n
Untuk rumus yang satu ini, mari ambil contoh soal sebagai berikut:
4√36 = 36/4
8. Pangkat Nol
Untuk sifat yang satu ini akan berlaku ketentuan a0 = 1. Bilangan berapapun kalau diberi pangkat 0 hasilnya akan tetap 1. Ambil contoh begini 50, ini bisa juga ditulis menjadi:
51-1 = 51 x 5-1 = 51 x i/51 = 51/51 = 1
Tetapi inipun dengan catatan bahwa nilai a itu tidak boleh sama dengan angka 0. Alasannya adalah kalau a = 0 maka akan menjadi 00 sehingga hasilnya menjadi tidak terdefinisi. Bahkan ketika dihitung dengan kalkulator pun tidak akan ada hasilnya.
Nah, penjelasan dan contoh sifat-sifat eksponen di atas harus kamu pahami dengan betul. Jangan sampai tertukar karena adakalanya dalam satu soal, berlaku beberapa sifat eksponen sekaligus. Kalau kamu tidak paham dengan ini, maka kamu akan kebingungan menyelesaikan soal tersebut.
Penerapan Sifat-Sifat Eksponen Dalam Kehidupan Sehari-Hari
Sifat-sifat eksponen adalah rumus yang sebenarnya sangat dekat dengan kehidupan sehari-hari walaupun memang tidak semua orang merasakannya. Sifat-sifat ini sendiri memang sangat membantu khususnya dalam memecahkan masalah dalam berbagai bidang.
Makanya, materi ini sangat penting juga untuk dipelajari. Bahkan, penggunaan sifat-sifat ini bisa ditemukan dalam bidang biologi, dalam bidang ekonomi dan dalam bidang sosial. Penjelasannya sebagai berikut:
1. Dalam Biologi
Kalau dalam bidang biologi, sifat-sifat bilangan berpangkat sering sekali dimanfaatkan untuk menghitung pertumbuhan bakteri. Untuk bidang yang satu ini, mari ambil contoh sebagai berikut:
Sebuah amoeba jumlahnya bisa bertambah dalam waktu tertentu karena amoeba akan tumbuh dengan cara membelah diri. Rumus eksponensial yang dipakai dalam hal ini ialah At = A0 x (2)t. A0 = 40 saat pukul 09.00 pagi. Pertanyaannya, ada berapa amoeba pukul 09.08 kemudian?
Penyelesaian :
A0 = jumlah amoeba dan t = lama pengamatan
At = A0 x (2)t = 100 x (2)8 = 100 x 256
At = 25.600
Artinya, hanya dalam kurun waktu 8 menit saja jumlah amoeba tersebut bisa mencapai 25.600
2. Dalam Ekonomi
Selain di bidang Biologi, eksponensial juga biasa diterapkan di bidang ekonomi. Kalau di bidang ekonomi biasanya penerapan eksponensial adalah di sektor perbankan dan investasi. Contoh kasusnya seperti ini.
Anggap saja kamu ingin berinvestasi dengan cara membeli saham di perusahaan A. Harga saham tersebut konsisten naik hingga 20% setiap tahunnya. Kalau kamu membeli saham yang harganya Rp1 juta, maka 5 tahun yang akan datang uang kamu akan menjadi Rp2.488.320.
Hal ini terjadi sesuai dengan informasi dalam tabel berikut:
| Tahun Ke | 0 | 1 | 2 | 3 | 4 | 5 |
| Total Uang | Rp1.000.000 | Rp1.200.000 | Rp1.440.000 | Rp1.728.000 | Rp2.073.600 | Rp2.488.320 |
Perlu diperhatian bahwa peningkatan sebesar Rp20% itu dihitungnya dari total uang yang diterima pada tahun terakhir ya, bukan pada tahun awal yang nilainya hanya Rp1 juta. Proses peningkatan sebesar 20% ini akan terus berlangsung secara konsisten.
Kecuali kalau kemudian ada kasus di mana harga saham menjadi turun dan keuntungan yang kamu dapat berada di bawah 20%. Peningkatan eksponensial seperti ini kalau di ekonomi biasa disebut dengan compound interest.
Mengetahui berapa keuntungan yang akan didapat dari investasi sebenarnya juga menjelaskan kenapa eksponen itu begitu penting dipelajari. Konsep bilangan berpangkat ini akan sangat terlihat dari perkalian keuntungan yang didapat setiap tahun.
Alasannya adalah karena seperti yang sudah disebutkan sebelumnya, eksponen itu metode perkalian yang berulang dan dalam contoh di atas keuntungan yang didapat juga berulang.
3. Bidang Sosial
Kalau di bidang sosial, materi tentang eksponen ini banyak digunakan untuk menghitung dan mengestimasi pertumbuhan penduduk dalam jangka waktu tertentu. Ambil contoh kasus seperti ini.
Tahun 2017, jumlah penduduk wilayah A sekitar 286.841 jiwa. Berapa jumlah penduduk di wilayah tersebut pada tahun 2027 jika laju pertumbuhan penduduknya sebesar 2,99%?
Untuk menyelesaikan soal seperti itu, kamu perlu memakai rumus laju pertumbuhan penduduk yang biasanya
Pt = P0ert dan keterangannya sebagai berikut
Pt : Perkiraan jumlah penduduk pada tahun 2027
P0 : Jumlah penduduk tahun 2017 sebesar 286.841 jiwa
t : Jangka waktu
r : Laju pertumbuhan penduduk
e : Bilangan eksponensial yaitu 2,71828182
Dari apa yang sudah diketahui di atas, selanjutnya tinggal menerapkan rumus tersebut sehingga penyelesaiannya menjadi seperti ini:
Pt= P0ert
Pt = 286.841 x e0,0299 x 10
Pt = 286.841 x 1.34850962347291
Pt = 386.807
Contoh Soal Sifat-Sifat Eksponen
Seperti yang sudah disampaikan sebelumnya, soal eksponen itu biasanya tidak hanya terdiri atas satu sifat saja, melainkan beberapa sifat sekaligus. Hal ini membuat kamu wajib paham dengan semua aturan sifat bilangan berpangkat agar lebih mudah mengerjakannya.
Untuk latihan kali ini, mari ambil contoh seperti ini.
Berapa hasil dari (8a3)2 ÷ 4a4 =
Dari contoh tersebut, bisa dituliskan cara penyelesaiannya sebagai berikut:
82 x (a3)2 ÷ 2a4 (pangkat 3 dikalikan pangkat 2 sehingga hasilnya 6 dan ditulis seperti di bawah ini)
64xa6÷4xa4 = 16a2 (64 langsung dibagi dengan 4 karena sejenis dan menghasilkan angka 16, kemudian untuk pangkat 6 akan dikurangi pangkat 4 sesuai dengan ketentuan sifat bilangan eksponen yaitu jika berada dalam bentuk pembagian, maka operasi hitung pangkat adalah dikurangi)
Sebagai kesimpulan, eksponen itu merupakan bilangan yang berupa perkalian dan ini sama hingga berulang kali. Agar lebih paham dengan eksponen ini, maka kamu perlu memperhatikan berbagai sifat bilangan berpangkat atau eksponen tersebut.
Perbanyak juga mengerjakan latihan soal sifat-sifat eksponen untuk memperdalam pemahaman. Karena kebanyakan yang muncul dalam soal adalah kombinasi dari beberapa sifat eksponen sekaligus, bukan hanya satu sifat saja.
Baca Juga: